Gli
articoli devono essere inviati in triplice copia cartacea e con un
dischetto a uno dei seguenti indirizzi: 1.
De Nuccio Sergio, via IV Novembre 24 – 86100
Campobasso.
2. Caserio
Antonio, via Leopardi 118 – 86100 Campobasso. Sono
accettati anche invii tramite e-mail ai seguenti indirizzi:
1. sedenuc@tin.it
; 2. ancser@yahoo.it
Il
lavoro deve essere scritto in Word e, di norma, non può superare
1 pagina (due colonne). TITOLO: al centro; carattere Arial;
dimensione 9; grassetto . AUTORI:
al centro; carattere Arial; dimensione 9 – TESTO: giustificato a
sinistra e a destra; carattere Times New Roman; dimensione 9;
interlinea singola. IL
GENIO RIBELLE: ÉVARISTE GALOIS di
Sergio De Nuccio –
Campobasso La
mattina del 31 maggio 1832, all’ospedale Cochin di Parigi moriva,
poco più che ventenne, Évariste Galois. La sua morte, causata da
una grave ferita all’addome riportata in un duello alla pistola
all’alba del giorno precedente, significò un’immensa perdita
per la Matematica. Molti
grandi matematici dell’800 sono pari a Galois per genialità;
nessuno, però, lo supera per l’originalità e la profondità
delle sue idee. Certamente la Teoria delle equazioni algebriche segnò
un progresso considerevole per i contributi di Lagrange, Gauss e
Abel, ma nessuno di questi riuscì a mettere in evidenza l’elemento
fondamentale da cui dipendono tutte le proprietà delle equazioni.
Il genio matematico di Galois si manifestò in tutta la sua
grandezza proprio quando, all’età di 18 anni, riuscì a
dimostrare che le caratteristiche essenziali di un’equazione
algebrica, compresa la sua risolubilità per mezzo di radicali, si
riflettono in specifiche proprietà di un particolare gruppo di
sostituzioni, che si accompagna all’equazione in esame e che
oggi viene chiamato gruppo di Galois di quella equazione. La
teoria dei gruppi di sostituzione già era stata oggetto di numerose
ricerche; ma, la generalizzazione del concetto di gruppo nella sua
accezione moderna la si deve a Galois, che nei suoi studi sulla
teoria delle equazioni fece emergere l’importanza della nozione di
sottogruppo normale e la fondamentale distinzione tra gruppi
semplici e gruppi composti. Évariste
Galois era nato il 25 ottobre 1811 a Bourge-la-Reine, un piccolo
sobborgo di Parigi, dove trascorse la sua infanzia fino all’età
di 12 anni, istruito
dalla madre che gli insegnò il latino e il greco. Nel
1823 fu ammesso a frequentare la quarta classe presso il Collegio
Reale Louis-le-Grand di Parigi, dove rimase come alunno
interno fino al 1829. Nei primi anni scolastici, Galois era un
alunno distinto e brillante; partecipava alle edizioni del Concours
général, ricevendo
premi e menzioni sia in matematica che in greco. All’età di 15
anni cominciarono a manifestarsi le sue straordinarie attitudini per
la matematica; s’immerse completamente nello studio delle Opere
classiche di Legendre e di Lagrange, trascurando tutte le altre
materie. A 17 anni pubblicò negli Annales di Gergonne il suo
primo lavoro: dimostrazione di un teorema sulle frazioni continue
periodiche,. Successivamente presentò all’Académie des
Sciences di Parigi due Memorie sulla risolubilità per mezzo di
radicali delle equazioni algebriche che, però, inspiegabilmente
vennero smarrite. Il lavoro matematico più importante tra quelli
pubblicati quando era ancora in vita, apparve nel 1830 nel Bulletin
de Férussac. Le altre Memorie fondamentali, ritrovate nelle sue
carte, furono pubblicate da Liouville nel 1846. Dopo aver tentato,
senza successo, per due volte l’esame di ammissione all’École
polythecnique, Galois entrò nel 1829 nell’École Normale,
da cui fu espulso l’anno successivo per motivi politici. Nell’ultimo
anno della sua vita si dedicò completamente alla politica e
trascorse molti mesi in carcere. “Sembra, ohimè!, che l’infelice
giovinetto abbia tristemente pagato il prezzo del suo genio”. Alla
vigilia del mortale duello, nella notte del 29 maggio 1823, come se
fosse consapevole della sua tragica fine, Galois scrisse il suo testamento
scientifico in una lettera al suo amico A. Chevalier. In esso
espose, tra le altre cose, i risultati essenziali delle sue ricerche
sugli integrali abeliani, che Riemann riuscì ad ottenere
venticinque anni più tardi.
NUMERI
ALLO SPECCHIO di
Antonio Salmeri – Roma In
un qualsiasi sistema numerico a base b > 2, il sistema
formato dalle cifre 1,
0, b-2, b-1 moltiplicato per k (k<b) e per b-k
produce sempre due numeri aventi le cifre poste in posizione
speculare: k,
k-1, b-k-1, b-k e
b-k, b-k-1, k-1, k. Si
ha infatti:
Nel
sistema decimale (b = 10) il numero
RIFLESSIONI SULLA CONGRUENZA TRA
TRIANGOLI
di
Francesco Laudano (Liceo
Scientifico A. Romita – CB) Esistono almeno due buone ragioni per riflettere sulla con
gru-enza (o isometria) tra triangoli. Innanzi tutto il concetto di
congruenza assume un ruolo importante nello sviluppo delle facoltà
logico-intuitive degli studenti. Inoltre la geometria euclidea è,
per buona parte, geometria della congruenza, poiché studia
proprietà invarianti per congruenze. Riflettendo sulla congruenza si osserverà che enunciati
poco rigorosi del secondo criterio generalizzato fanno cadere in
errore e generano false convinzioni. Per evitare ciò si propongono
dei controesempi mediante costruzioni che potrebbero trovare spazio
tra le attività didattiche. 1.
Alcuni controesempi Come è ben noto, grazie ai criteri di congruenza, per
accertare la congruenza tra due triangoli è sufficiente disporre di
informazioni “appropriate” sulla congruenza di alcuni elementi
dei due triangoli. Spesso la presenza di tre elementi
rispettivamente congruenti comporta la congruenza degli altri tre.
Ma non sempre ciò avviene, e, per quanto banale, è utile mostrare
esempi di triangoli simili ma non congruenti. Sembrerebbe, però,
quasi evidente che due triangoli aventi quattro elementi
rispettivamente congruenti debbano essere congruenti, visto che
almeno uno degli elementi congruenti deve essere un lato. Ma nemmeno
questo è vero. Prop 2. E’ possibile
costruire due triangoli non congruenti aventi quattro elementi
rispettivamente congruenti. Dim: basta considerare un triangolo rettangolo G e
suddividerlo tracciando l’altezza relativa all’ipotenusa in due
triangoli rettangoli S e D. Oltre all’angolo retto, S e G hanno un
lato ed un angolo acuto in comune (ma non sono congruenti).
L’osservazione precedente potrebbe essere generalizzata a
triangoli scaleni qualunque. Per quanto banale, quest’osservazione induce a riflettere
sugli enunciati dei criteri di congruenza dei triangoli, ed in
particolare sul secondo criterio e sulle sue conseguenze. Molti
testi, infatti, enunciano e “dimostrano” un criterio secondo il
quale: “Due triangoli sono congruenti se hanno congruenti due
angoli e un lato”. Il controesempio fornito in precedenza mostra che l’affermazione
appena citata è falsa. Per scoprire il paradosso è necessario
analizzare con attenzione la dimostrazione del secondo criterio,
valutando esattamente le ipotesi implicite del suo enunciato. Si
comprende, allora, che essa non può essere replicata sui triangoli
del controesempio poiché i loro lati rispettivamente congruenti non
sono opportunamente posti. In altri termini per condurre a buon fine
la dimostrazione è necessario che i lati congruenti siano opposti
ad angoli rispettivamente congruenti! Molti testi, antichi e nuovi,
per indicare questa circostanza, usano premettere l’avverbio “ordinatamente”
all’aggettivo congruenti. In conclusione è corretto affermare
che: Due triangoli sono congruenti se hanno due angoli e un lato
ordinatamente congruenti. A
questo punto sorge spontanea la domanda seguente: esistono coppie di
triangoli non congruenti aventi cinque elementi rispettiva-mente
congruenti? Alcuni studi svolti dal prof.
Pennini (Cfr.
M.Pennisi, Triangles et moyennes, Mathematique &
pedagogie n. 99, 21-26, 1994),
hanno consentito di rispondere affermativamente a questa domanda. Per fornire agli studenti uno
spunto concreto per una riflessione sui criteri di congruenza, e
sgomberare il campo da false convinzioni, può essere utile cercare
una semplice costruzione di una siffatta coppia di triangoli.. La
costruzione che si propone nella prossima proposizione utilizza la
parte aurea di un segmento, pertanto nel disegno compaiono anche gli
elementi necessari alla costruzione della parte aurea. Prop 3. E’ possibile
costruire due triangoli non congruenti aventi cinque elementi
rispettivamente congruenti.
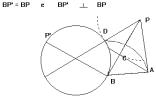
Si punti il compasso in B con
apertura uguale alla lunghezza di PC e si tracci la circonferenza
. Si tracci inoltre la retta
r per
C perpendicolare a PB.
ed r si intersecano in due punti (essendo PC>BC), detto A uno
di essi lo si congiunga con P e con B. Osservazione: il triangolo PAB è
rettangolo in A. Infatti esso ha l’angolo in B in comune col
triangolo ABC, e per costruzione si ha
PB : AB = AB : BC . Quindi PAB e ABC sono simili per
avere un angolo congruente compreso tra lati proporzionali. Di
conseguenza l’angolo PAB è retto. Dall’osservazione precedente si deduce
che i triangoli PAC e PAB hanno cinque elementi congruenti. Si può inoltre osservare che
anche i triangoli PAC ed ABC hanno cinque elementi congruenti.
UNA COSTRUZIONE DI ENRICO D’OVIDIO di
Antonio Caserio – Liceo
Artistico “G. Manzù” - CB L’insegnamento della geometria razionale nella
scuola attuale è talmente ridotto che difficilmente il docente
affronta il classico problema della quadratura del cerchio. Tuttavia
egli, se volesse approfondire l’argomento, potrebbe presentare
agli studenti una costruzione geometrica del grande matematico
campobassano Enrico D’Ovidio, semplice e ingegnosa, che fornisce
un quadrato la cui area approssima grandemente quella di un dato
cerchio. Infatti, come è noto il problema non si può risolvere
esattamente con riga e compasso. La costruzione è esposta nel testo Elementi
di Geometria (1) che D’Ovidio (1843-1933) pubblicò nel 1869,
assieme al Sannia, e per la sua originalità è riportata anche nell’enciclopedia
Questioni riguardanti le
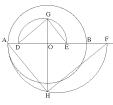
matematiche elementari di Federigo Enriques. Costruzione
di D’Ovidio
Dim.
Posto AO = r, per la costruzione fatta, si ha:
E poiché il lato del quadrato equivalente al cerchio dato è r . 1,7724674 , GH differisce da esso, per eccesso, per meno di
, dato che
Si
osservi anche che
Note (1)
Questo testo di geometria elementare per i licei ebbe 14 edizioni e
rimase in adozione per oltre 50 anni nelle scuole italiane. |

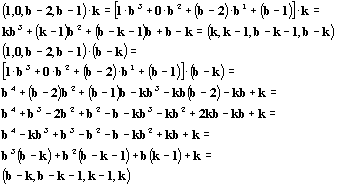 Si deduce che il numero
Si deduce che il numero