|
Il
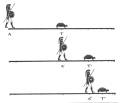
paradosso di Achille e la tartaruga “Il
piè veloce Achille non potrà mai raggiungere la tartaruga, se
questa ha un vantaggio iniziale, per quanto piccolo”.
|
MathMese Pubblicazione
mensile della sezione Mathesis “E. D’Ovidio” – Campobasso DIRETTORE RESPONSABILE:
Filippo Poleggi – CAPO
REDAZIONE: Sergio
De Nuccio – SEGRETARIO
DI REDAZIONE:
Antonio Caserio – REDAZIONE:A. Antinucci,
A. Aquilino, F. Laudano, E. Lustrato, R. Raucci. G. Vitullo. REGISTRAZIONE: Tribunale
di Campobasso n° 276
del 20 maggio 2002 SEDE: Scuola
elementare “E. D’Ovidio” – via Roma, 41
- 86100
Campobasso Gli articoli devono essere
inviati in triplice copia cartacea e con un dischetto o per e-mail
a: 1.
De Nuccio Sergio, via IV Novembre 24 – 86100
Campobasso. E-MAIL:
sedenuc@tin.it 2.
Caserio Antonio, via
Leopardi 118 – 86100 Campobasso. E-MAIL: ancser@yahoo.it |
Anno I, Numero 3 Luglio
2002 Zenone
di Elea (490
ca – 430 aC.) |
Il
lavoro deve essere scritto in Word e, di norma, non può superare 1
pagina (due colonne). TITOLO: al centro; carattere Arial; dimensione 9;
grassetto .
AUTORI:
al centro; carattere Arial; dimensione 8 – TESTO: giustificato a
sinistra e a destra; carattere Times New Roman; dimensione 9; interlinea
singola.
UN PARADOSSO SUI TRIANGOLI EUCLIDEI
di
Francesco Laudano
(Liceo
Scientifico A. Romita – CB)
Alcuni anni fa, durante un corso
di aggiornamento residenziale, una avvenente collega siciliana, della
quale purtroppo non ricordo il nome, mi propose uno strano
“esercizio”. Si trattava di scovare l’errore in una dimostrazione di
geometria euclidea che conduceva ad una tesi paradossale[1].
La questione è tanto semplice da poter essere presentata ad alunni delle
classi prime delle superiori. Tuttavia essa può suscitare profonde
riflessioni epistemologiche, sul rapporto tra l’aspetto formale degli
enunciati di geometria euclidea e la loro interpretazione. Mi è parso
opportuno, quindi, dopo aver riveduto ed approfondito il paradosso,
riproporlo a colleghi ed alunni.
1.
Il
paradosso
Per rendere più fluido la
sviluppo della dimostrazione, sarà utile ricordare due semplici enunciati
di geometria del piano.
Prop 1. L’asse di un segmento
è il luogo dei punti del piano equidistanti dagli estremi del segmento.
Prop 2. La bisettrice di un angolo è il luogo dei punti del piano
equidistanti dai lati dell’angolo.
E’ superfluo sottolineare che
queste proposizioni, presenti su tutti i testi di geometria euclidea, sono
incontestabilmente vere.
Ed eccoci alla proposizione
paradossale. Per rendere più intrigante lo sviluppo dell’argomentazione
ne lascio incompleto l’enunciato. Sarà completato dopo averne data la
dimostrazione.
Prop 3. Tutti i triangoli sono
…………………….
 dim:
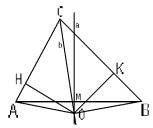
Sia ABC un triangolo non isoscele, e siano a
l’asse del segmento AB e b
la bisettrice dell’angolo in C.
dim:
Sia ABC un triangolo non isoscele, e siano a
l’asse del segmento AB e b
la bisettrice dell’angolo in C.
Si osservi, innanzi tutto, che a e b debbono necessariamente incontrarsi. Se così non fosse, infatti, la bisettrice b (essendo parallela all’asse a) dividerebbe il triangolo ABC in due triangoli rettangoli ADC e BDC. Questi triangoli, avendo anche gli angoli ACD e BCD congruenti ed il lato CD in comune sarebbero congruenti. Di conseguenza il triangolo ABC sarebbe isoscele. Dunque, poiché stiamo considerando un triangolo ABC non isoscele, a e b debbono necessariamente incontrarsi. Sia O il loro punto d’intersezione.
La parte successiva del ragionamento sarà sviluppata suppo-nendo che il punto O non sia interno al triangolo ABC. Se O si suppone interno si può ragionare in modo analogo.
Poiché il punto O appartiene all’asse a, per la proposizione 1 i segmenti AO e BO sono congruenti. Quindi, se O è esterno al triangolo ABC, il triangolo AOB è isoscele. Pertanto gli angoli OAB ed OBA sono congruenti.
Siano H e K, rispettivamente, le proiezioni di O su AC e su BC. Poiché O appartiene alla bisettrice b, per la proposizione 2, OH ed OK sono congruenti. Quindi i triangoli AOH e BOK risultano congruenti per il criterio di congruenza dei triangoli rettangoli. Infatti, essi, oltre all’angolo retto, hanno congruenti le ipotenuse AO ed OB ed i cateti OH ed OK. Di conseguenza gli angoli OAH ed OBK sono congruenti.
Quindi se O si trova sul segmento AB il triangolo ABC risulta isoscele. Se, invece O è esterno al triangolo ABC, con riferimento alla figura disegnata, si è dimostrato che:
1. gli angoli OAH ed OBK sono congruenti,
2. gli angoli OAB e OBA sono congruenti.
Dunque, per differenza di angoli congruenti, risultano congruenti anche gli angoli BAC e ABC.
Si è, quindi, dimostrato che il triangolo (non isoscele) ABC è, in ogni caso, isoscele! In altre parole: tutti i triangoli sono isosceli. Come si spiega questo paradosso?
![]()
UN PRESIDENTE MATEMATICO
di Antonio Caserio
( Liceo Artistico “G. Manzù” – CB)
È opinione
di tutti gli storici che il teorema di Pitagora (1) abbia rappresentato
una delle scoperte più importanti della matematica antica, comune del
resto a quasi tutte le civiltà. Le innovazioni che da esso derivarono
furono moltissime sia nel campo applicativo (agrimensura, costruzione di
edifici ecc.) sia nel campo astratto (geometria teorica, aritmetica
superiore, numeri irrazionali ecc.). La sua importanza non doveva essere
sfuggita nemmeno a Pitagora tanto che la leggenda racconta che egli, per
celebrarne la scoperta, fece sacrificare cento buoi agli dei (2). Il
teorema, dunque, è meritatamente famoso e si può affermare,
senz’altro, che abbia interessato chiunque si sia accostato, nel corso
della sua vita, alla matematica.
Ne è la conferma un libro interamente dedicato al teorema, che la dottoressa Elisha Scott Loomis pubblicò nel 1940. Nel testo The Pythagorean Proposition, scaturito dalla sua passione per la matematica, la dottoressa raccolse tutte le differenti dimostrazioni allora note del teorema, oltre 370. Si va da matematici di chiara fama (Bhaskara, Fibonacci, Wallis, Huyghens, Leibniz, De Morgan ma anche Leonardo) a perfetti sconosciuti o dilettanti.
Fra le tante
dimostrazioni presenti nel libro è degna di essere conosciuta, per la sua
semplicità, quella escogitata, nel 1876, da
James Abram Garfield (1831 - 1881), ventesimo
presidente degli Stati Uniti (3).
Illustriamo,
nel seguito, questa piacevole dimostrazione che sembra l’unico
contributo dato alla matematica da un presidente americano.
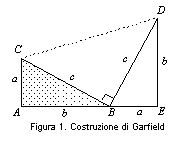
Sia
BAC un triangolo rettangolo in A,
avente i cateti AC e AB lunghi
rispettivamente a e b mentre l’ipotenusa BC
è lunga c. Si costruisca sul
prolungamento del cateto AB il
triangolo BED, rettangolo in E,
congruente a BAC con BE = AC,
come in figura 1. Si congiunga, quindi, il vertice C
con D in modo da ottenere il
trapezio rettangolo AEDC.
Si osservi
che il triangolo CBD è isoscele
e rettangolo in B, poiché
l’angolo
![]() è supplementare dei due
angoli
è supplementare dei due
angoli
![]() e
e
![]() , tra loro complementari.
, tra loro complementari.
Si determini,
ora, l’area del trapezio AEDC
nei seguenti modi:
(i)
Area (AEDC) =
Area (ABC) + Area (CBD)
+ Area (BEC) =
![]() ;
;
(ii) Area
(AEDC) =
![]() =
=
![]() =
=
![]() =
=
![]() .
.
Dall’uguaglianza
![]() =
=
![]() dei due risultati, si deduce
quindi:
dei due risultati, si deduce
quindi:
![]()
che esprime
la relazione di Pitagora per le misure dei lati del triangolo rettangolo
dato.
Garfield
medesimo raccontò di avere trovato la dimostrazione in un momento di
pausa dei lavori del Congresso, dopo un’accesa discussione
sull’ordine del giorno, e che fu l’unica cosa in cui al termine tutti
i deputati, senza distinzione di partito, furono d’accordo!
Non resta da
dire che questa dimostrazione del celebre teorema è alla portata di
chiunque sappia calcolare il quadrato di un binomio e determinare l’area
di un trapezio.
Note
(1) È appena
il caso di ricordare che il teorema afferma che in
un qualunque triangolo rettangolo il quadrato costruito sull’ipotenusa
è equivalente alla somma dei quadrati costruiti sui cateti.
(2) Con ironia, qualche bello spirito subito
osservò che, da quel giorno, trema la razza dei buoi ogni volta che un
matematico scopre una verità.
(3) Garfield, nato ad Orange nell’Ohio,
combatté nell’esercito unionista durante la guerra di secessione
americana e divenne generale nel 1863. Successivamente fu deputato e
senatore del suo Stato e si batté per la ricostruzione del Sud sconfitto
e per i diritti dei negri. Eletto presidente
nel novembre del 1880 fu assassinato qualche mese dopo, ad Elberon
nel New Jersey, da un assiduo postulante.
![]()
UN
POSSIBILE APPROCCIO ALLA LOGICA
di
Sergio De Nuccio - Campobasso
Introduzione
-. Da molti anni i programmi di matematica di ogni ordine scolastico
prevedono l’insegnamento di alcuni argomenti di Logica, che nel biennio
delle scuole secondarie superiori sono: la logica delle proposizioni;
proposizioni elementari e connettivi; valore di verità di una
proposizione composta; inferenza logica, principali regole di deduzione;
variabili, predicati, quantificatori.
Nei
commenti ai programmi viene raccomandato esplicitamente di
trattare questi argomenti in modo da abituare lo
studente a esprimersi correttamente, a ragionare con rigore
logico, a sentire la necessità di tradurre idee intuitive in
concetti formali.
Dopo
tanti anni di sperimentazione si avverte la sensazione che questi
suggerimenti siano stati quasi completamente ignorati. Sembra che per la Logica
si sia ripetuta l’esperienza negativa dell’Insiemistica. Questo
argomento, un tempo enfatizzato e spesso incompreso, nella pratica
didattica è stato sempre trattato come un semplice insieme di regole che
riguardano i diagrammi di Eulero-Venn. Allo stesso modo si è identificata
la Logica con la Logica proposizionale e, quasi sempre,
quest’ultima è stata trattata come un insieme di regole per la
compilazione delle tavole di verità di espressione proposizionali più o
meno ricche di connettivi. Salvo qualche rara eccezione, nei manuali
scolastici più diffusi gli argomenti di logica sono stati culturalmente
isolati, trattati come oggetti a sé stanti in un capitolo
all’inizio o alla fine del testo. In questo modo è venuta meno la
possibilità di guidare gli insegnanti, meno preparati sul tema, a
progettare uno specifico percorso didattico, sfruttando anche le numerose
occasioni offerte da molti
argomenti tradizionali.
Ciò
che vogliamo proporre in questo articolo e nei successivi è un diverso
approccio agli argomenti di logica, che tenga conto delle raccomandazioni
contenute nel commento al tema. E’ un modo di trattare la Logica,
a livello di biennio, che si basa sulla consapevolezza che, mentre la
matematica si esprime in un linguaggio, in logica il linguaggio
stesso è oggetto di studio. All’inizio la logica viene
vista come Scienza delle regole del linguaggio e in seguito come Scienza
del ragionamento corretto.
Con la collaborazione dell’insegnante di
Lettere, si programmano alcune lezioni per analizzare la struttura
sintattica e semantica di un linguaggio naturale, per poi introdurre
opportune ipotesi di lavoro che consentano di costruire, a partire da
quest’ultimo, il linguaggio della Logica proposizionale e della Logica
dei predicati. Il percoso didattico deve attuarsi con riferimenti
storici significativi per dare allo studente brevi notizie sull’origine
e sugli sviluppi successivi della Logica.
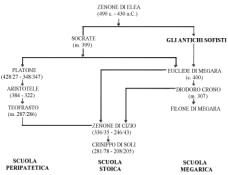 La
Logica greca.
– Per Aristotele, Zenone di Elea era il fondatore della dialettica,
ma i primi filosofi che s’interessarono a problemi di logica furono due
allievi di Socrate: Euclide di Megara e Platone. Aristotele, allievo di
Platone, elaborò la Teoria del sillogismo, che doveva essere una
teoria generale dell’inferenza. In realtà, questa teoria non è poi così
generale perché si limita a codificare una classe di inferenze che hanno una
struttura del tutto particolare. Essa rappresenta una piccola parte della
cosiddetta Logica dei predicati monadici in cui le proposizioni
vengono analizzate secondo la struttura soggetto-predicato, con
l’ipotesi che ogni predicato possa applicarsi ad un solo soggetto.
Assente quasi del tutto nella teoria aristotelica del sillogismo è la Logica
proposizionale che tratta dei connettivi logici. Essa è
una sottoteoria della logica dei predicati ed ebbe origine con i Megarici
e gli Stoici. La scuola megarica, fondata da Euclide di Megara,
precedette quella stoica, perchè i fondatori di quest’ultima,
Zenone di Cizio e Crisippo di Soli, impararono la loro logica dai megarici
Diodoro Crono e Filone di Megara. La logica megarico-stoica si sviluppò
contemporaneamente e parallelamente alla logica di Aristotele, ma con
differenze abbastanza marcate. La prima è, come si è detto, una logica
delle proposizioni mentre la seconda è una logica dei termini; la prima
è costituita esclusivamente di regole, mentre la seconda di leggi;
Aristotele, da allievo di Platone, cerca le essenze e quindi risponde alla
domanda: “A appartiene a B?”, i Megarici, invece, partono dalla
domanda preplatonica: “Come si può confutare l’enunciato p?”.
(continua).
La
Logica greca.
– Per Aristotele, Zenone di Elea era il fondatore della dialettica,
ma i primi filosofi che s’interessarono a problemi di logica furono due
allievi di Socrate: Euclide di Megara e Platone. Aristotele, allievo di
Platone, elaborò la Teoria del sillogismo, che doveva essere una
teoria generale dell’inferenza. In realtà, questa teoria non è poi così
generale perché si limita a codificare una classe di inferenze che hanno una
struttura del tutto particolare. Essa rappresenta una piccola parte della
cosiddetta Logica dei predicati monadici in cui le proposizioni
vengono analizzate secondo la struttura soggetto-predicato, con
l’ipotesi che ogni predicato possa applicarsi ad un solo soggetto.
Assente quasi del tutto nella teoria aristotelica del sillogismo è la Logica
proposizionale che tratta dei connettivi logici. Essa è
una sottoteoria della logica dei predicati ed ebbe origine con i Megarici
e gli Stoici. La scuola megarica, fondata da Euclide di Megara,
precedette quella stoica, perchè i fondatori di quest’ultima,
Zenone di Cizio e Crisippo di Soli, impararono la loro logica dai megarici
Diodoro Crono e Filone di Megara. La logica megarico-stoica si sviluppò
contemporaneamente e parallelamente alla logica di Aristotele, ma con
differenze abbastanza marcate. La prima è, come si è detto, una logica
delle proposizioni mentre la seconda è una logica dei termini; la prima
è costituita esclusivamente di regole, mentre la seconda di leggi;
Aristotele, da allievo di Platone, cerca le essenze e quindi risponde alla
domanda: “A appartiene a B?”, i Megarici, invece, partono dalla
domanda preplatonica: “Come si può confutare l’enunciato p?”.
(continua).
[1]
Cfr. YA. S.
Dubnov “Errori nelle
dimostrazioni di geometria”, P.T.E.-Milano, Esempio 6, pag. 12 ,
1965.